ProbTree

結果が定まっていない実験や観察を1回行うこと。

例1）「コインを1枚投げて、それが表か裏かを確認する」

例2）「さいころを1回振って、出た目を見る」

例3）「くじびきを1回ひく」

これらの1回ずつの行為は全て試行であり、思考の結果として起こる事柄を事象と呼ぶ。

試行によって起こり得る結果（事柄）、またはその集まりのこと。

例）「コインを1枚投げて、それが表か裏かを確認する」という試行を5回行う。

この時、コインが示す結果は「表が出る」か「裏が出る」の2通りであり、それぞれこの試行の事象である。

つまり、「この試行の全事象を答えよ」と問われれば、「表が出るという事象と裏が出るという事象の２つ」と答えられる。

ある事柄が起こる可能性について、すべてのパターンを数え上げた総数のこと。◯◯通りと数える。

例）「2枚のコインを投げる時、起こりうる全ての場合の数を答えよ」

2枚のコイン（AとB）を投げる時、その出方は以下に示す通り。

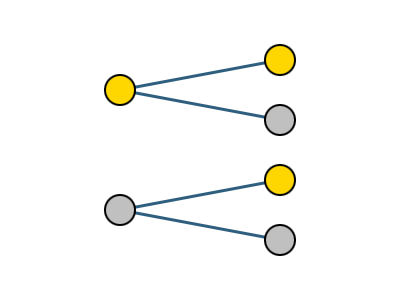
起こりうる全てのパターンは4つあるため、この場合の数は「4通り」である。

1回あるいは複数回の試行において、特定の事象が起こる可能性の高さを数値で表したもの。「特定の事象の場合の数」を「全事象の場合の数」で割ることで求められる。

例）「2枚のコインを投げる時、両方とも表である確率を答えよ。」

2枚のコイン（AとB）を投げる時、その出方は以下に示す通り。

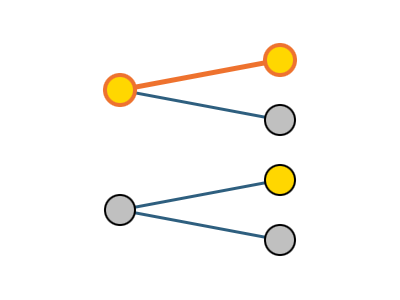
すべての場合の数は4通りであり、そのうち2枚とも表であるのは1通りであるため、この確率は「1/4 (25%)」である。

1回あるいは複数回の試行において、想定されるすべての事象を木の枝のように枝分かれしていく図で表すこと。

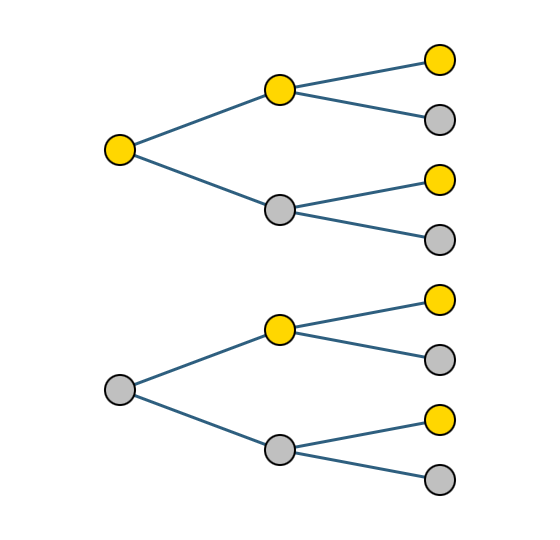
例）「コインを3回投げる時、起こりうるすべて事象を樹形図で表せ。」

起こりうるすべての事象を書き出すと、以下に示す8通り。

「表」を黄色い丸、「裏」を灰色の丸とし、樹形図を描くと次のようになる。